Blog -




Machine Learning 101: An Engineer’s Perspective
In 2019, FloQast released a product called AutoRec, which automates the account reconciliation process, saving accountants hours or days they would otherwise spend manually sifting through transactions each month to identify true exceptions or reconciling items. This is often achieved by comparing two data sets, such as the general ledger against the bank statement.
In order to accomplish that task, we developed a matching engine that used numerous algorithms to comb through the data and automatically match transactions on behalf of the user. But, as the number of AutoRec users increased, so did the number of variations in how matches are made for different clients. This led to a growing number of configuration options and increased complexity in the engine, as well as a growing number of custom configurations that had to be maintained for individual clients. We needed a more scalable solution!
So, we asked ourselves, can we use machine learning here? At the time, I was new to the engine team and had no experience with machine learning. I had more questions than answers.

Even today, there are a number of questions about machine learning (and quite a few misnomers, as well) and its capabilities. So, I’ll attempt to help you build a basic intuition for what machine learning is and how it works.
A (Very) Brief Introduction to Machine Learning
The term “machine learning” has become immensely popular in the last few years, but it’s not always clear what exactly is being “learned” and how. And while this is a vast field of study with many different techniques, algorithms, and applications, we’ll use a simple example to illustrate the core concept which is at the heart of machine learning.
Let’s begin with how we humans may learn from data that we’re presented with. Suppose you were given the following data and asked to figure out what the values for A and B might be:
(A x 2) + ( B x 10) = 30
(A x 3) + ( B x 20) = 55
(A x 5) + ( B x 30) = 85
You probably correctly arrived at the conclusion that A = 5 and B = 2 [Editor’s Note: It was my understanding that there would be no math…]. Now, think about the process that took place in your mind as you were solving the problem. It may have looked something like this:
- Take a guess at initial values for A and B
- Calculate the result for each line using the selected values
- Check the results against the given answers
- Adjust values for A and B and repeat until the results match the answers (as best as possible)
We have just described a training loop! The same process is used in machine learning, where the goal is to learn the optimal values for A and B (also known as weights) based on the given answers. And since we are given the answers to check against, this is called supervised learning.
In this example, we have two input features, the values [2, 3, 5] and [10, 20, 30], that correspond to the weights A and B, respectively, but in reality, there could be hundreds or thousands of features that represent different pieces of data. The features are the data points that describe the problem you’re trying to solve. So, if you were trying to predict housing prices, your features might include things like square footage, number of bedrooms, number of bathrooms, etc…
Of course, that begs the question:

How exactly does the machine know how to mimic the above process of guessing and adjusting the weights?
As it turns out, there are algorithms that know just how to do that! In fact, machine learning is essentially a set of established algorithms that make learning possible. One such algorithm is called gradient descent. The initial weights may start with zeros or random values. The more interesting part is how it adjusts the weights to get closer to the correct answers by minimizing the cost (the difference between the current results and the given answers) with each iteration. It does so using formulas based on derivatives to determine whether each weight should be increased or decreased.
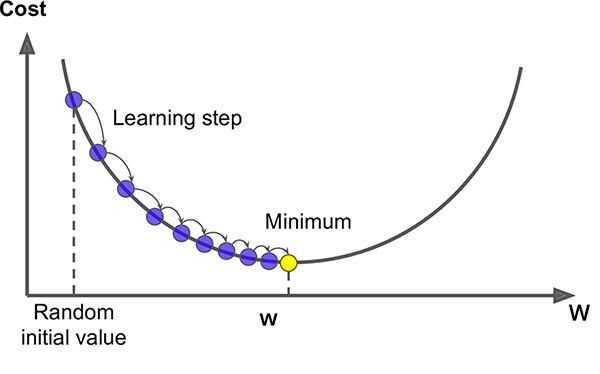
Now that we learned the optimal weights based on the given input data (also known as training data), we have a model (Read: Set of weights) that can be used to predict the output for new data for which we don’t have the answers.
You may also have a binary classification problem in which the training answers are either 1 (yes) or 0 (no) and the model will be trained to predict a value (also known as a probability) between 0 and 1, in which case you might consider a probability of 0.5 or higher to be a yes prediction.
Back to Our Transaction Matching Problem
If we step back and look at what machine learning is doing, it’s learning the relative importance (weight) of the individual features in relation to the output being predicted.
So for the matching engine, we realized that if we could come up with a way (i.e. features) to represent what a matching pair of transactions looks like, we can use machine learning to train a model that can predict if we have a match. And better yet: We don’t have to use custom configuration to account for the variations across FloQast users because the model can learn these variations all on its own, and we end up with virtually a zero-configuration matching engine that doesn’t have to increase in complexity as more clients use it.
It also makes life easier for our clients and our support team because they no longer have to look at the data and try to come up with their own set of matching rules, which must be designed and maintained by the user, to produce the best matches.
Back to Blog
